[ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ]

(Related publications: [PUBLink] [PUBLink])

As an example of the application of local search with global constraints, we look at the dynamic job-shop scheduling problem.

The problem of solving standard job-shop scheduling by local search has been addressed in numerous research papers (see [PUBLink] for a survey), but there are few experiments dealing with a partial satisfaction/infeasible state neighborhood. Experiments including dynamic aspects of job addition/removal are also rare. This is a pity since dynamics and partial satisfaction are very realistic problem features and local search approaches can bring their advantages to bear in these domains particularly.

As in traditional n × m job-shop scheduling, there are n jobs in a schedule, each of them having m tasks with fixed durations. All tasks of a job are connected via m - 1 linear distance inequalities involving start or end time points of two tasks. For compliance with the scheduling horizon h, there is in addition a linear distance inequality taskend <= h for each task. Each task has to be processed on a specific machine, and each of the o machines can process only one task at a time. Every p microseconds of computation time, one job is removed from the schedule and a new job must be added. The tasks of the new job are randomly distributed within the scheduling horizon.

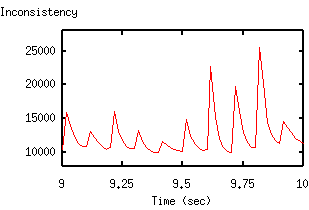
The goal is to find a concrete begin/end for all currently active tasks, such that the inconsistency of the constraints is as low as possible. To compare different algorithms, the inconsistency can be displayed over time (see figure below; peaks occur on job removal/addition) and the average inconsistency can be computed.

The measurement of inconsistency is done in the following way:

• For each discrete point of time from 0 to h on each machine, the number of assigned tasks - 1 is added to the inconsistency if there is an assignment of more than one task.
• For each linear distance inequality that is unsatisfied, the minimal shift distance for one of the inequality variables required to satisfy the inequality is added to the inconsistency.

The initial state for the test runs is computed by the iterative addition of n jobs, with p microseconds of computation time between each addition, which is used for improvement iterations.

The following parameters were used for the test runs throughout our experiments: The tasks' duration is 100 plus a random value of -99 to +100. 40% of a job's tasks require the same machine as another of the job's tasks. The jobs' inequalities consist of 20% equations and 80% real inequalities. The inequalities involve a shift constant, which is 100 plus a random value of -99 to +100.

• Realization
• Results
• Constraint Weights

For questions, comments or suggestions, please contact us.

Last update:
May 19, 2001 by Alexander Nareyek