| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [ENHANCEMENT] | [Durations] [Optimization] [Dynamics] [Other Extensions] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publication: [PUBLink])
The feature of being able to handle dynamic changes of the problem specification is also very important for the computer-games domain because goods, their destinations and transportation facilities vary over time.
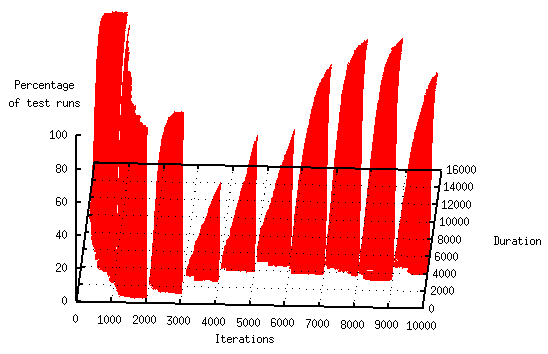
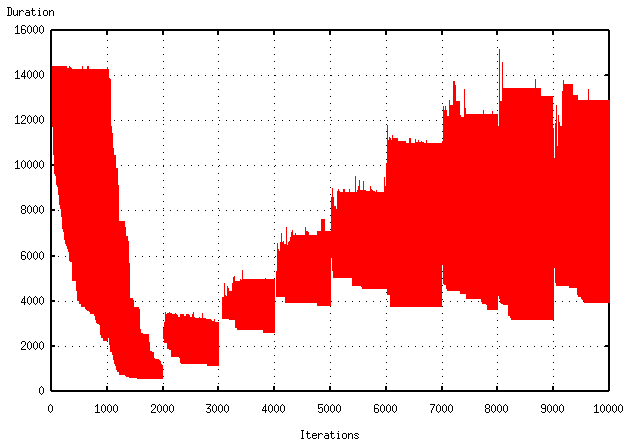
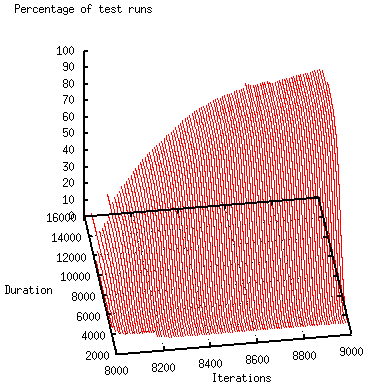
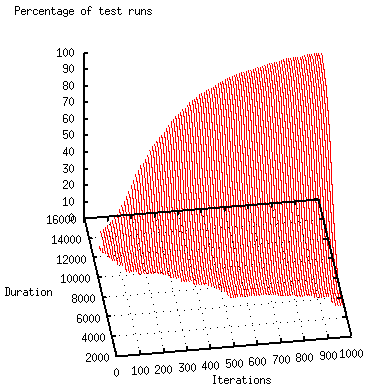
To test the approach's ability to handle dynamics, a random package is canceled every 1,000 iterations (no matter if it is already on the way or has been delivered) and a new package is inserted (its initial location and destination being decided at random). The time point for the Begin variables of the Precondition Tasks of the SGoals's Task Constraint is increased by MaximallyNecessaryActionsPerPackage × MaximalActionLength + 1, i.e., for the 6-1 modifications, by 12 × 200 + 1 = 2401, to ensure the existence of a satisfiable plan. The figure below shows the results for Problem 6-1a. The optimization can quickly recover after a change takes place (the second figure shows the view from above).

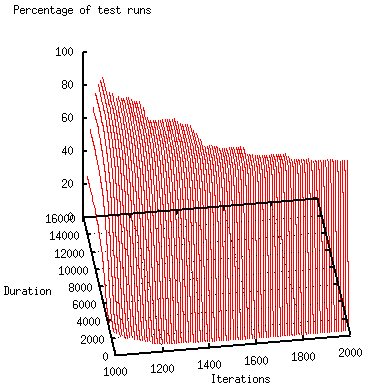
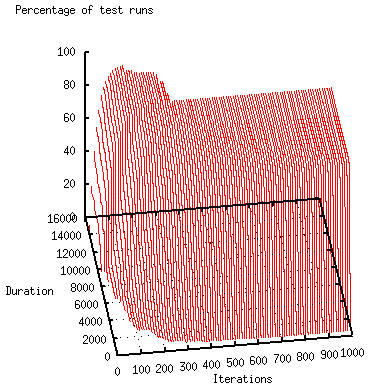
The figures below (dynamic adaptation on the left; recomputation on the right) contrast cuttings of the dynamic solution with test runs in which the computation was restarted from scratch for a change. It is clear that the dynamic adaptation converges much more quickly. Larger problems and higher dynamics can mean that a problem cannot even be tackled by a recomputation from scratch because there is not enough time for a regeneration of the problem's representation.
| [ENHANCEMENT] | [Durations] [Optimization] [Dynamics] [Other Extensions] |
For questions, comments or suggestions, please contact us.
Last update:
May 20, 2001 by Alexander Nareyek