| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [SEARCH FRAMEWORKS] | [Operations Research] [Propositional Satisfiability] [Constraint Programming] [Discussion] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publication: [PUBLink])
Operations research (OR) is a collection of techniques developed to handle industrial optimization problems. With our problem domain, we have mostly finite decision variables (there is no continuous transition between doing something or not). Continuous variables are only used for specific states (see also Chapter [Model]). The eligible operations-research methods for this domain are integer programming (IP) and mixed-integer programming (MIP) [PUBLink]. Problems are usually formulated using the following mathematical framework:
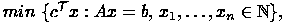
where c is the cost vector, x the vector of the decision variables x1 ... xn, and cTx the cost function that is to be minimized with respect to the equation system Ax = b. The decision variables have to be natural numbers, but in the case of MIP some of the variables can also be non-negative real numbers.
The solution methods are based on techniques like Simplex [PUBLink] and interior-point methods [PUBLink]. These approaches solve a linear relaxation of the problem (dropping the integrality constraints). Afterwards, the system is strengthened in order to enforce the integrality constraints, e.g., by a branch-and-bound with cutting planes.
There are only a few approaches for solving planning problems with OR methods. These include a domain-dependent approach by Bockmayr and Dimopoulos [PUBLink], ILP-PLAN by Kautz and Walser [PUBLink] and the state-change formulations by Vossen et al. [PUBLink].
| [SEARCH FRAMEWORKS] | [Operations Research] [Propositional Satisfiability] [Constraint Programming] [Discussion] |
For questions, comments or suggestions, please contact us.
Last update:
May 19, 2001 by Alexander Nareyek