EXCALIBUR
Adaptive Constraint-Based Agents in Artificial Environments |
|
[ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ]
|
Constraint Programming
(Related publication:
[PUBLink])
Unlike OR and SAT, constraint programming uses a much more declarative and
general specification. Problems are formulated in a framework of variables,
domains and constraints. The constraint satisfaction problem (CSP) consists of
- a set of variables x = {x1, ... ,
xn}
- where each variable is associated with a domain
d1, ..., dn
- and a set of constraints c = {c1,
..., cm} over these variables.
The domains can be symbols as well as numbers, continuous or discrete (e.g.,
"door", "13", "6.5"). Constraints are relations between variables (e.g.,
"xa is a friend of
xb",
"xa <
xb ×
xc") that restrict the
possible value assignments. Constraint satisfaction is the search for
a variable assignment that satisfies the given constraints. Constraint
satisfaction is the search for a variable assignment that satisfies the
given constraints. Constraint optimization requires an additional function
that assigns a quality value to a solution and tries to find a solution
that maximizes this value. A brief example of constraint programming is given
here.
A satisfaction can be achieved by refinement as well as local-search approaches,
already presented in Section
[Search Paradigms].
In the usual refinement approach, the variables are labeled (an assignment of a
domain value) one after the other. In the case of an inconsistency (a constraint
is violated), backtracking is triggered. Numerous variable and value ordering
heuristics have been proposed, such as smallest-domain-first or
smallest-value-first
[PUBLink]. There are also generalized
labeling techniques, in which the value selection is replaced by a domain
reduction [PUBLink] and variable-
and value-selection strategies with a stronger interleaving
[PUBLink]. In addition, there are many
extensions and modifications of naive backtracking
[PUBLink]
[PUBLink]
[PUBLink], some of them being analyzed in
[PUBLink].
The propagation of the refinement consequences is usually achieved by so-called
consistency techniques. For example, we have two variables A and B
with domains of {1 ... 10} and a constraint B > A. In the case of
a refinement of A
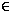 {5 ... 10}, the propagation will entail a domain reduction of B to
{6 ... 10}. The propagation can be made globally or locally. A global
propagation analyzes all consequences within the constraint system and is very
costly to compute. Local propagation is therefore usually applied, the
consequences here being propagated only partially. Numerous local-propagation
methods are available, such as arc-consistency algorithms like AC-4
[PUBLink] and AC-7
[PUBLink], or path consistency
algorithms like PC-4 [PUBLink].
{5 ... 10}, the propagation will entail a domain reduction of B to
{6 ... 10}. The propagation can be made globally or locally. A global
propagation analyzes all consequences within the constraint system and is very
costly to compute. Local propagation is therefore usually applied, the
consequences here being propagated only partially. Numerous local-propagation
methods are available, such as arc-consistency algorithms like AC-4
[PUBLink] and AC-7
[PUBLink], or path consistency
algorithms like PC-4 [PUBLink].
Satisfaction mechanisms based on local search are not very popular so far.
This may be due to the traditional logic-programming framework for constraint
programming. Nevertheless, many new methods have been proposed, especially
in the last years. This includes Hirayama and Toyoda's coalition forming
[PUBLink] and the well-known
min-conflicts heuristic for binary CSPs by Minton et al.
[PUBLink] with its extension and
generalization in GENET by Davenport et al.
[PUBLink].
Applications of constraint programming to planning include Descartes [PUBLink], parcPLAN [PUBLink], CPlan [PUBLink], the approach of Rintanen and Jungholt [PUBLink] and GP-CSP [PUBLink].
For questions, comments or suggestions, please contact us.
Last update:
May 19, 2001 by Alexander Nareyek
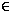 {5 ... 10}, the propagation will entail a domain reduction of B to
{6 ... 10}. The propagation can be made globally or locally. A global
propagation analyzes all consequences within the constraint system and is very
costly to compute. Local propagation is therefore usually applied, the
consequences here being propagated only partially. Numerous local-propagation
methods are available, such as arc-consistency algorithms like AC-4
[PUBLink] and AC-7
[PUBLink], or path consistency
algorithms like PC-4 [PUBLink].
{5 ... 10}, the propagation will entail a domain reduction of B to
{6 ... 10}. The propagation can be made globally or locally. A global
propagation analyzes all consequences within the constraint system and is very
costly to compute. Local propagation is therefore usually applied, the
consequences here being propagated only partially. Numerous local-propagation
methods are available, such as arc-consistency algorithms like AC-4
[PUBLink] and AC-7
[PUBLink], or path consistency
algorithms like PC-4 [PUBLink].