| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [LOCAL] | [Global] [Granularity] [Control] [Job-Shop] [Minima] [Extension] [Conclusion] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publications: [PUBLink] [PUBLink])
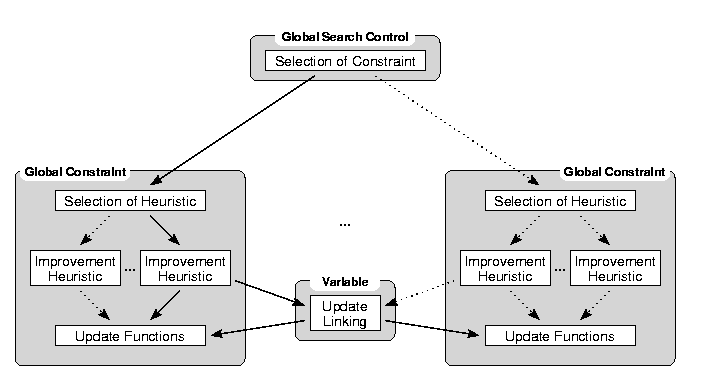
As described above, global constraints have integrated heuristics to enable them to choose a successor state on their own. On top of the constraints, there must be a mechanism that combines the constraints' cost contributions to the overall cost function and a regulation determining which constraint is allowed to select the successor state for a current iteration. This is the job of the global search control. The components' interplay is outlined in the following figure.

The global search control serves as a general manager, to which variables and constraints can dock on and off in a plug-and-play manner. This provides a simple mechanism for tackling problems with dynamic changes. To add a new variable, the variable in question must already be instantiated. To add a constraint, the constraint's inclusion of a variable must be announced to the variable to allow the constraint's updating in the case of value changes.
For the overall cost function, which is handled by the global search control, problem-specific coefficients can be introduced to weight the constraints' subjective costs, as a constraint's importance may be different in different contexts (see also Section [Constraint Weights]).
Conventional local search methods make a successor decision on the basis of a calculation of the neighborhood states' costs. These calculations might be quite costly to compute within the global constraint framework, but the current constraints' costs can serve as an excellent compensation for this. As the goal is to minimize the constraints' costs and as the global constraints should know how to resolve the conflicts by themselves, it is a straightforward matter to select constraints according to their current inconsistency.
The selection of the global constraint that is to improve the current state can be enhanced by various meta-heuristics to avoid local minima and plateaus, ranging from a simple random choice of unsatisfied constraints to more elaborate techniques including learning, tabu lists, etc. Some of these are demonstrated in the following section's case study. The global search control module should support a variety of methods that can be applied in a user-specified way (as in the flexible blackbox system [PUBLink]). By integrating global search-state parameters for the constraints' improvement procedures, e.g., a simulated-annealing-like temperature, an anytime improvement depending on the current search situation can be achieved. In addition, it is possible to introduce higher-level coordination mechanisms between constraints to minimize violations of multi-constraint variables. If knowledge is available about these interface areas, it may be sufficient to introduce redundant global constraints to cover these areas. Nevertheless, the overhead of coordination mechanisms may pay off in some cases.
| [LOCAL] | [Global] [Granularity] [Control] [Job-Shop] [Minima] [Extension] [Conclusion] |
For questions, comments or suggestions, please contact us.
Last update:
May 19, 2001 by Alexander Nareyek