| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [SCSP] | [Grammars] [Elements] [Structural Constraints] [SCSPs] [Generation] [Redundancy] [Combination] [Conclusion] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publication: [PUBLink])
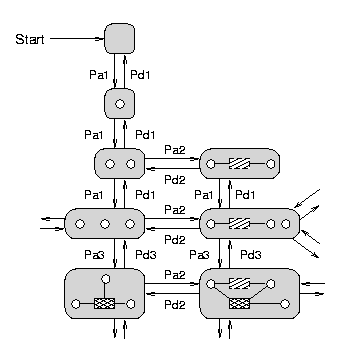
For conventional constraint satisfaction, values are assigned to variables. This builds the search tree/space with potential solutions. In contrast, structural constraint satisfaction uses productions to create constraint graphs. The figure below shows an example of a search space for an SCSP.

It must be guaranteed that all valid constraint graphs can be constructed by the productions. For refinement search, an empty start graph can continuously be expand toward a possible constraint graph by addition productions for the single elements (see [PUBLink] for structural constraint satisfaction approaches for refinement search). For local search techniques, these addition productions are not sufficient as any state must be reachable from any other state and not only from the empty start graph. This requirement can be satisfied by the introduction of further deletion productions:
Requirement reqp: The effect of an addition production can be retracted by a directly following application of a corresponding deletion production.
Analogously to the constraint checking in conventional constraint satisfaction, an SCSP's structural constraints have to be checked during search. The productions, together with the structural constraints, provide a tool to allow search to generate and verify a solution. However, the search space is potentially infinite and the support of preemptive alternative reductions and domain-specific search knowledge about which production to apply and where to apply it on is very important (like propagation/consistency methods and variable- and value-ordering heuristics in conventional constraint satisfaction). This is elaborated in Section [Combination with the Global Constraint Approach].
The following subsections provide rules to create productions that can add/delete all potential graph elements. In the same way as values that are not in the domains of variables are not considered in conventional constraint satisfaction, graphs that violate the SCSP's embedding and extension graphs are implicitly prevented by the productions.
| [SCSP] | [Grammars] [Elements] [Structural Constraints] [SCSPs] [Generation] [Redundancy] [Combination] [Conclusion] |
For questions, comments or suggestions, please contact us.
Last update:
May 20, 2001 by Alexander Nareyek