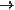 V, and associate a label to every vertex and edge,
lv : V
V, and associate a label to every vertex and edge,
lv : V 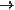 L and le : E
L and le : E
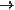 L. The
figure below shows an example graph.
L. The
figure below shows an example graph.
| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [SCSP] | [Grammars] [Elements] [Structural Constraints] [SCSPs] [Generation] [Redundancy] [Combination] [Conclusion] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publications: [PUBLink] [PUBLink] [PUBLink])
This section provides a more or less informal introduction in algebraic graph grammars (see [PUBLink] [PUBLink] [PUBLink] for a detailed overview).
Algebraic graph grammars are a generalization of Chomsky grammars. A graph
signature GSig consists of the sorts of vertices V, edges E,
and a label alphabet L. The operations of GSig provide source and
target vertices for every edge, s, t : E 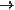 V, and associate a label to every vertex and edge,
lv : V
V, and associate a label to every vertex and edge,
lv : V 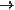 L and le : E
L and le : E
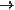 L. The
figure below shows an example graph.
L. The
figure below shows an example graph.
A match m of graph g1 to graph g2 is a total graph morphism that maps the vertices and edges of g1 to g2 such that the graphical structure and the labels are preserved. We use injective matches only.
A production P is a partial morphism between a left-hand side Pl and a right-hand side Pr, which provides information about which elements are preserved, deleted and created in the case of an application of the production. The identity of objects is marked by appended identifiers like :1 (see figure below). A production is applicable to a graph g, if there is a match of Pl to g. The figure below shows an example of a production. A general vertex that can match any vertex is graphically depicted by a flat ellipse with a dotted outline. A general edge that can match any edge is graphically depicted by a dotted line.
A derivation g2 of g1 is the so-called push-out graph of an application of an applicable production P. The new graph g2 is similar to g1, but the elements of Pr that are not in Pl are added, and elements of Pl that are not in Pr are deleted. We formulate a general requirement for the deletion of vertices as it would be unclear how to proceed with dangling edges:
Requirement reqd: A production can specify the deletion of a vertex only if the vertex has no edge to another vertex.
The figure below shows how the graph of the first figure above can be transformed using the production of the second figure.
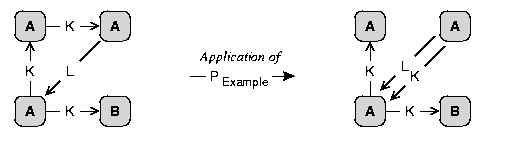
The application of a production may also require application conditions.
A negative application condition (NAC) is a total morphism
C: Pl
 n
that is satisfied for a match L: Pl
n
that is satisfied for a match L: Pl
 g
such that there is no morphism G: n
g
such that there is no morphism G: n
 g
such that G · C = L.
An NAC is represented by a convex dark area (e.g., in the production of the
figure above). A positive application condition (PAC) is a total
morphism C: Pl
g
such that G · C = L.
An NAC is represented by a convex dark area (e.g., in the production of the
figure above). A positive application condition (PAC) is a total
morphism C: Pl
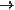 p that is
satisfied for a match L: Pl
p that is
satisfied for a match L: Pl
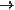 g
if there is a morphism G: p
g
if there is a morphism G: p
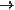 g such that
G · C = L. A PAC is represented by a convex light area (e.g., in
left-hand side of the figure of
Section [Avoiding Redundancy]). For
multiple application conditions, such as in production
PMachinee of the
figure of Section
[Productions for Constraint Extensions],
the conjunction of the conditions must hold.
g such that
G · C = L. A PAC is represented by a convex light area (e.g., in
left-hand side of the figure of
Section [Avoiding Redundancy]). For
multiple application conditions, such as in production
PMachinee of the
figure of Section
[Productions for Constraint Extensions],
the conjunction of the conditions must hold.
Graph grammars can be used as a mechanism for describing potential neighbor states in the search space. This neighborhood is composed of all possible direct derivations of the current graph. The whole search space, such as the Cartesian product of all variables' domains in conventional CSPs, can be described by the corresponding graph language, with the empty graph as start graph.
| [SCSP] | [Grammars] [Elements] [Structural Constraints] [SCSPs] [Generation] [Redundancy] [Combination] [Conclusion] |
For questions, comments or suggestions, please contact us.
Last update:
May 20, 2001 by Alexander Nareyek