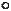
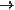
 )-connected variables to be a subset of
the set of (
)-connected variables to be a subset of
the set of (
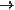
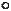 )-connected variables. The
pbase graph of a Subset constraint
includes two variables (
)-connected variables. The
pbase graph of a Subset constraint
includes two variables (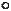
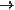

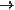
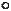 ), and there are two possible extensions corresponding
to the two possible variable connections.
), and there are two possible extensions corresponding
to the two possible variable connections.
| EXCALIBUR Adaptive Constraint-Based Agents in Artificial Environments |
| [SCSP] | [Grammars] [Elements] [Structural Constraints] [SCSPs] [Generation] [Redundancy] [Combination] [Conclusion] |
| [ Please note: The project has been discontinued as of May 31, 2005 and is superseded by the projects of the ii Labs. There won't be further updates to these pages. ] |
(Related publications: [PUBLink] [PUBLink])
The addition of nonextensible constraints prevents redundant constraints by means of a corresponding NAC in Pnonextensiblea-productions. This avoidance of redundancy is not ensured for extensible constraints. Generic structural constraints can overcome this problem.
A production for extending an extensible constraint Pextensiblee adds further edges to the graph. Extensible constraints of the same type must differ by involving at least one other (or additional) element. There must be a structural constraint Sextensible for each extensible constraint type, docking at each pair of potentially redundant constraints, and having all possible distinctive features as test alternatives.
Potentially redundant constraints are two constraints of the same type that are connected to the same elements according to the base graph pbase:
Construction Sextensible - docking part: The docking part of the structural constraint is created by two pbase graphs, where the corresponding vertices (without the constraints themselves) are unified. To avoid multiple redundant structural constraint instances per potentially redundant constraint pair, all but the constraints themselves are a PAC.
Possible distinctive features are vertices that are connected to one constraint but not (in the same way) to the other:
Construction Sextensible - testing part: There are two alternatives per unique edge (label; direction with respect to the constraint - toward it or away from it) that is included in the constraint's extension graphs. Each of the two alternatives consists of a graph with the two constraints of the docking part and an additional general vertex. Between each constraint and the general vertex is an edge corresponding to the unique edge. In the one alternative, the edge to the first constraint is an NAC; in the other alternative, the edge to the second constraint is an NAC.
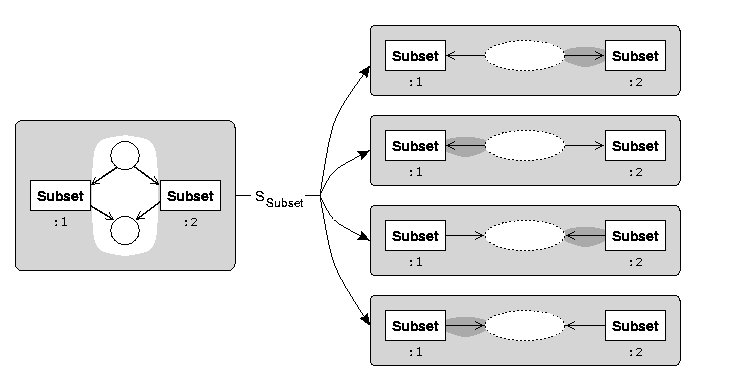
The figure below shows an example of a Subset constraint that forces the
set of (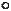
 )-connected variables to be a subset of
the set of (
)-connected variables to be a subset of
the set of (
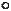 )-connected variables. The
pbase graph of a Subset constraint
includes two variables (
)-connected variables. The
pbase graph of a Subset constraint
includes two variables (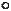

 ), and there are two possible extensions corresponding
to the two possible variable connections.
), and there are two possible extensions corresponding
to the two possible variable connections.
| [SCSP] | [Grammars] [Elements] [Structural Constraints] [SCSPs] [Generation] [Redundancy] [Combination] [Conclusion] |
For questions, comments or suggestions, please contact us.
Last update:
May 20, 2001 by Alexander Nareyek